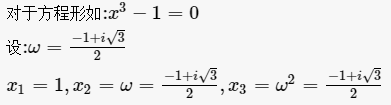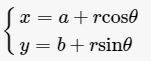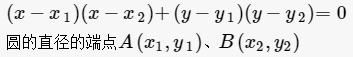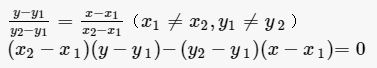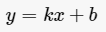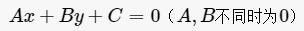只含有一个未知数(即“元”),并且未知数的最高次数为3次的整式方程。
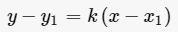
通过直线过的一个点和其斜率求该直线平面方程的一种方法。在平时做解析几何的题目时,会更多地运用点斜式方程来解题,直接的体现直线的性质。除此之外还有截距式,斜截式,两点式。其中截距不是距离,是一个数,可正,可负,可为零。
...
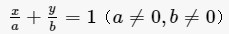
对x的截距就是y=0时,x 的值,对y的截距就是x=0时,y的值。截距就是直线与坐标轴的交点的横(纵)坐标。x截距为a,y截距b,截距式就是:x/a+y/b=1(a≠0且b≠0)。
...
随着奖励减少而导致态度逐渐消极,随着奖励增加而导致态度逐渐积极的心理现象,被称之为“阿伦森效应”。阿伦森效应也指人们最喜欢那些对自己的喜欢、奖励、赞扬不断增加的人或物,最不喜欢那些显得不断减少的人或物。 为什么会这样呢?其实主要是挫折感在作怪。从倍加褒奖到小的赞赏乃至不再赞扬...
酒与污水定律是指一匙酒倒进一桶污水,得到的是一桶污水;把一匙污水倒进一桶酒里,得到的还是一桶污水。显而易见,污水和酒的比例并不能决定这桶东西的性质,真正起决定作用的就是那一勺污水,只要有它,再多的酒都成了污水。酒与污水定律说明对于坏的组员或东西,要在其开始破坏之前及时处理掉。 几乎在任何组织里,都存...