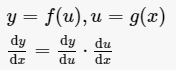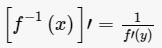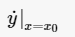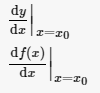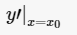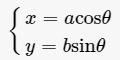设函数y=f(u)的定义域为Du,值域为Mu,函数u=g(x)的定义域为Dx,值域为Mx,如果Mx∩Du≠Ø,那么对于Mx∩Du内的任意一个x经过u;有唯一确定的y值与之对应,则变量x与y之间通过变量u形成的一种函数关系,这种函数称为复合函数。
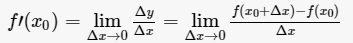
设函数y=f(x)在点x0的某个邻域内有定义,当自变量x在x0处有增量Δx,(x0+Δx)也在该邻域内时,相应地函数取得增量Δy=f(x0+Δx)-f(x0);如果Δy与Δx之比当Δx→0时极限存在,则称函数y=f(x)在点x0处可导,并称这个极限为函数y=f(x)在点x0处的导数。
...