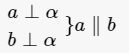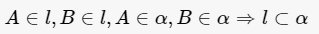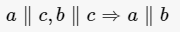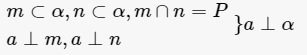
如果一条直线与一个平面内的任意一条直线都垂直，就说这条直线与此平面互相垂直。判定定理：如果一条直线与平面内两条相交直线都垂直，那么这条直线与这个平面垂直。
线面垂直的判定方法 1.线面垂直的判定定理:直线与平面内的两相交直线垂直。 2.面面垂直的性质:若两平面垂直则在一面内垂直于交线的直线必垂直于另一平面。 3.线面垂直的性质:两平行线中有一条与平面垂直,则另一条也与平面垂直。 4.面面平行的性质:一线垂直于二平行平面之一,则必垂直于另一平面。 5.定...
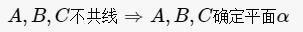
三个不在同一条直线上的点确定一个平面。两条相交直线确定一个平面。两条平行直线确定一个平面。一条直线与直线外的一点确定一个平面。
根据平行线的定义：在同一平面内没有公共点的两条直线叫做平行线。所以两条平行线一定在同一个平面内。再证明唯一性：在直线a上任取一点A，因为a平行于b，所以点A不在直线b上。根据平面基本性质的推论，经过一条直线和直线外的一点有且只有一个平面。所以经过点A和直线b的平面只有一个。因为经过直线a和直线b的平...
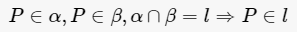
两个不重合的平面有一个公共点，叫做这两平面相交。在两个相交平面的交线上任取一点，经过此点在两个平面内作交线的垂线，二垂线所夹的锐角成为两平面的倾角。在两相交平面之一内作直线与交线成直角，当此直线与另一平面成直角时，则称两平面相交成直角。
...
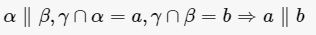
两个平面平行，在一个平面内的任意一条直线平行于另外一个平面。两个平行平面，分别和第三个平面相交，交线平行。两个平面平行，和一个平面垂直的直线必垂直于另外一个平面。
定理1：两个平面平行，在一个平面内的任意一条直线平行于另外一个平面。 定理2：两个平行平面，分别和第三个平面相交，交线平行。 定理3：两个平面平行，和一个平面垂直的直线必垂直于另外一个平面。（判定定理1的逆定理） 推论：两个平行平面的垂线平行或重合。 定理4：三个平行平面截两条直线，形成的对应线段成...
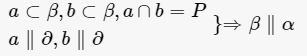
如果两个平面垂直于同一条直线，那么这两个平面平行。如果一个平面内有两条相交直线与另一个平面平行，那么这两个平面平行。如果一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行，那么这两个平面平行。
...
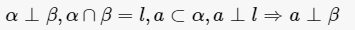
如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内等。
面面垂直的定义：若两个平面的二面角为直二面角(平面角是直角的二面角)，则这两个平面互相垂直。 面面垂直性质定理 1.如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。 2.如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。 3.如果两个...
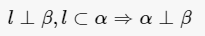
一条线与另一条线相交并成直角，这两条直线互相垂直。通常用符号“⊥”表示。
①在同一平面内，过一点有且只有一条直线与已知直线垂直。垂直一定会出现90°。 ②连接直线外一点与直线上各点的所有线段中，垂线段最短。简单说成：垂线段最短。 ③点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。...
1968年，美国科学史研究者罗伯特·莫顿（Robert K. Merton）提出这个术语用以概括一种社会心理现象：“相对于那些不知名的研究者，声名显赫的科学家通常得到更多的声望即使他们的成就是相似的，同样地，在同一个项目上，声誉通常给予那些已经出名的研究者，例如，一个奖项几...